转载自: https://houbb.github.io/2020/01/07/regex-and-dfa-02

有限状态机

有限状态机(Finite-state machine)，也被称为有限状态自动机(finite-state automation)，是表示有限个状态以及在这些状态之间的转移和动作等行为的数学计算模型(From 维基百科状态机) 。
听起来晦涩难懂，我用大白话描述一遍，状态机其实就是用图把状态和状态之间的关系描述出来，状态机中的一个状态可以在某些给定条件下变成另外一种状态。
举个很简单的例子你就懂了。比如我今年18岁，我现在就是处于18岁的状态，如果时间过了一年，我就变成19岁的状态了，再过一年就20了。当然我20岁时时光倒流2年我又可以回到18岁的状态。
这里我们就可以把我的年龄状态和时间流逝之间的关系用一个自动机表示出来，如下。

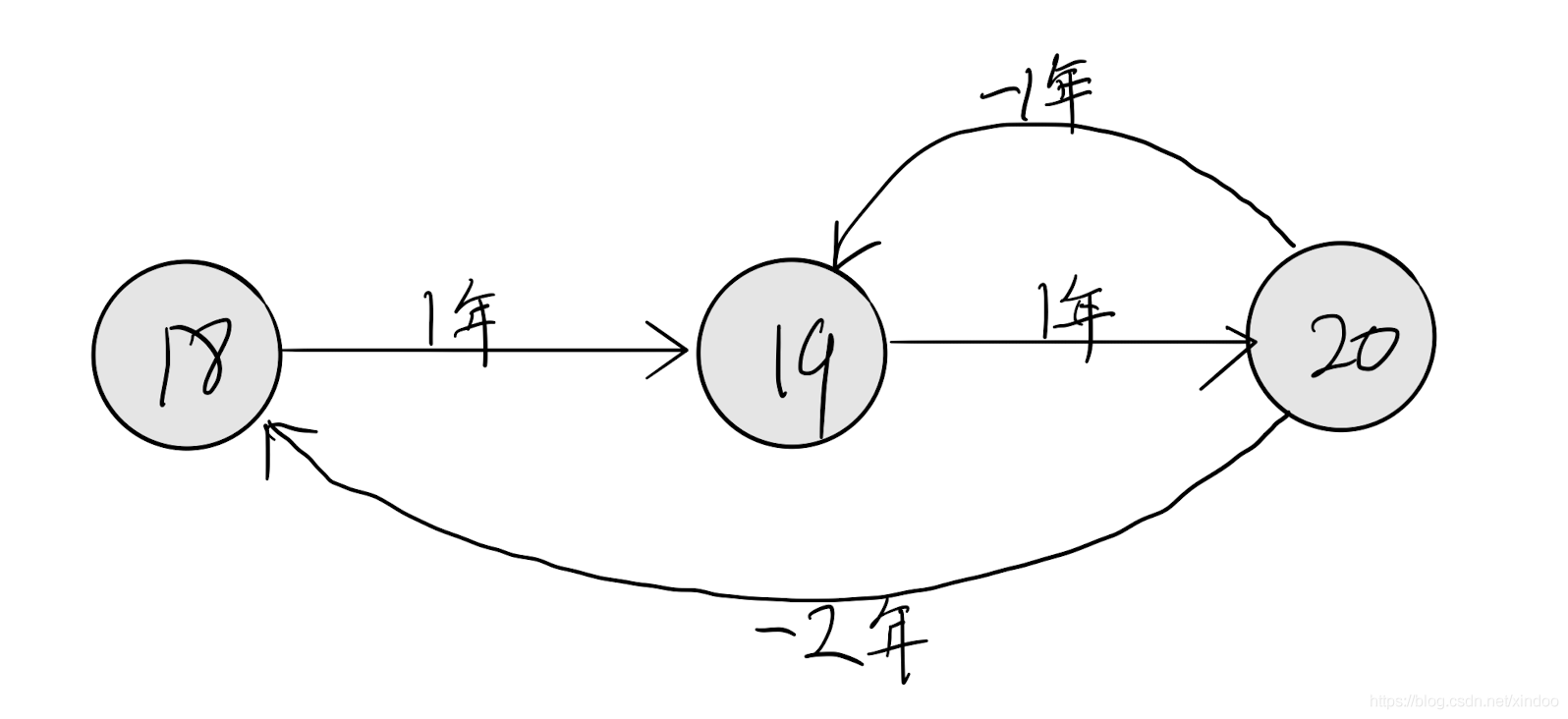
每个圈代表一个节点表示一种状态，每条有向边表示一个状态到另一个状态的转移条件。
上图中状态是我的年龄，边表示时间正向或者逆向流逝。
有了状态机之后，我们就可以用状态机来描述特定的模式，比如上图就是年龄随时间增长的模式。如果有人说我今年18岁，1年后就20岁了。照着上面的状态机我们来算下，1年后你才19岁，你这不是瞎说吗！没错，状态机可以来判定某些内容是否符合你状态机描述的模式了。哟，一不小心就快扯到正则表达式上了。

状态

我们这里再引入两种特殊的状态：**起始态和接受态(终止态)**，见名知意，不用我过多介绍了吧，起始态和终止态的符号如下。

字符串匹配

我们拿状态机来做个简单的字符串匹配。
比如我们有个字符串“zsx”，要判断其他字符串是否和”zxs”是一致的，我们可以为”zxs”先建立一个自动机，如下。

对于任意一个其他的字符串，我们从起始态0开始，如果下一个字符能匹配到0后边的边上就往后走，匹配不上就停止，一直重复，如果走到终止态3说明这个字符串和”zxs“一样。
任意字符串都可以转化成上述的状态机，其实到这里你就知道如何实现一个只支持字符串匹配的正则表达式引擎了，如果想支持更多的正则语义，我们要做的更多。

状态机下的正则表达式

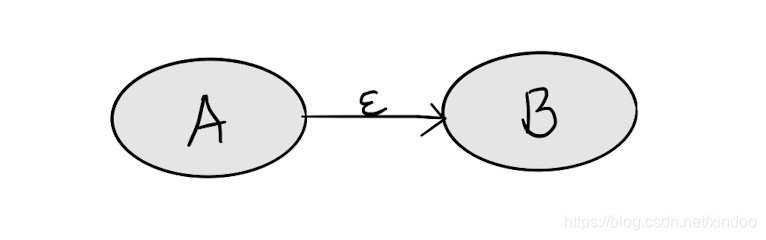
我们再来引入一条特殊的边，学名叫 __ϵ 闭包__，其实就是一条不需要任何条件就能转移状态的边。

没错，就只这条红边本边了，它在正则表达式状态机中起着非常重要的连接作用，可以不依赖其他条件直接跳转状态，也就是说在上图中你可以直接从1到2。
有了 ϵ 闭包的加持，我们就可以开始学如何画正则表达式文法对应的状态机了。

串联匹配

首先来看下纯字符匹配的自动机，其实上面已经给过一个”zxs”的例子了，这里再贴一下，其实就是简单地用字符串在一起而已，如果还有其他字符，就继续往后串。

两个表达式如何串在一起，也很简单，假如我们已经有两个表达式A B对应的状态机，我们只需要将其用 ϵ 串一起就行了。

并联匹配

正则表达式中的 | 标识二选一都可以，比如 A|B A能匹配 B也能匹配，那么 A|B 就可以表示为下面这样的状态图。

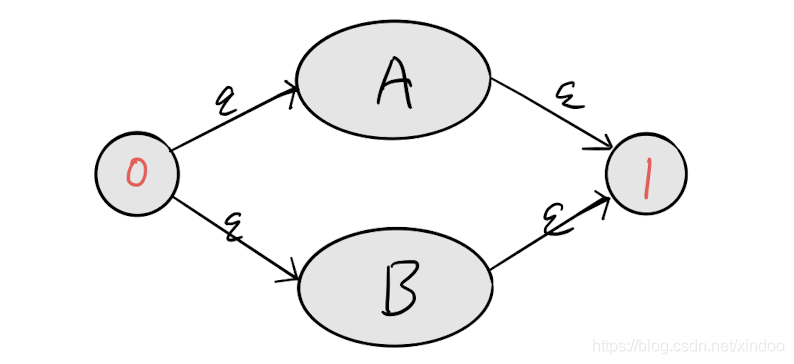
从0状态走A或B都可以到1状态，完美的诠释了A|B语义。
ps: 这里将表达式和图联系起来。一个或，就是两条路径都可以走通的意思。

重复匹配(正则表达式中的 ? + *)

正则表达式里有4种表示重复的方式，分别是：

?重复0-1次
+重复1次以上
*重复0次以上
{n,m} 重复n到m次

我来分别画下这4种方式如何在状态机里表示。
0-1 次

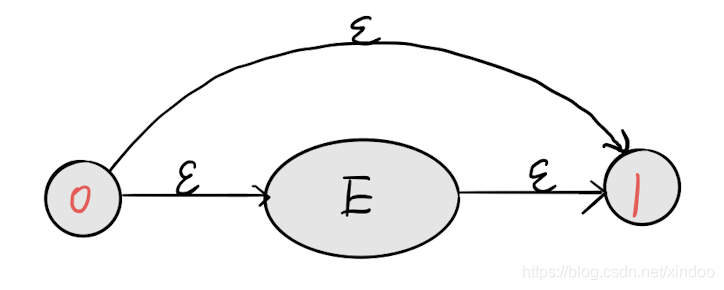
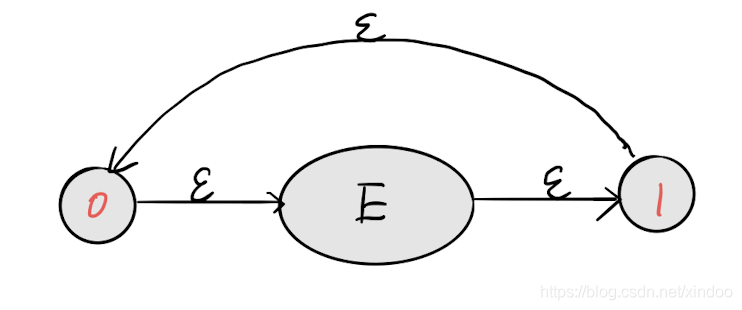
重复1次以上
0到1后可以再通过 ϵ 跳回来，就可以实现E的1次以上匹配了。

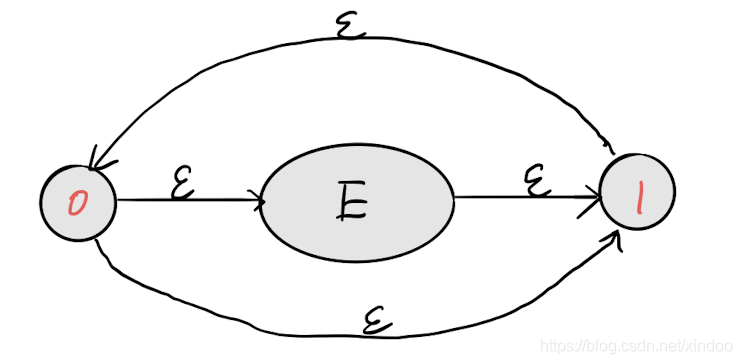
重复0次以上
其实就是 ? + 的结合。

匹配指定次数

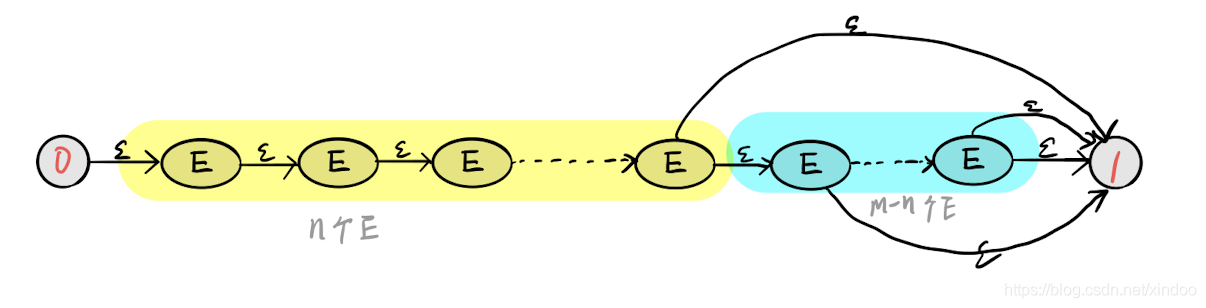
这种建图方式简单粗暴，但问题就是如果n和m很大的话，最后生成的状态图也会很大。
其实可以把指定次数的匹配做成一条特殊的边，可以极大减小图的大小。

特殊符号(正则表达式中的 . \d \s……)

正则表达式中还支持很多某类的字符，比如 . 表示任意非换行符，\d 标识数字，[] 可以指定字符集。
其实这些都和图的形态无关，只是某条特殊的边而已，自己实现的时候可以选择具体的实现方式，比如后面代码中我用了策略模式来实现不同的匹配策略，简化了正则引擎的代码。

子表达式(正则表达式 () )

子表达可以Thompson算法，其实就是用递归去生成 () 中的子图，然后把子图拼接到当前图上面。
（什么Thompson说的那么高大上，不就是递归吗！）

练习题

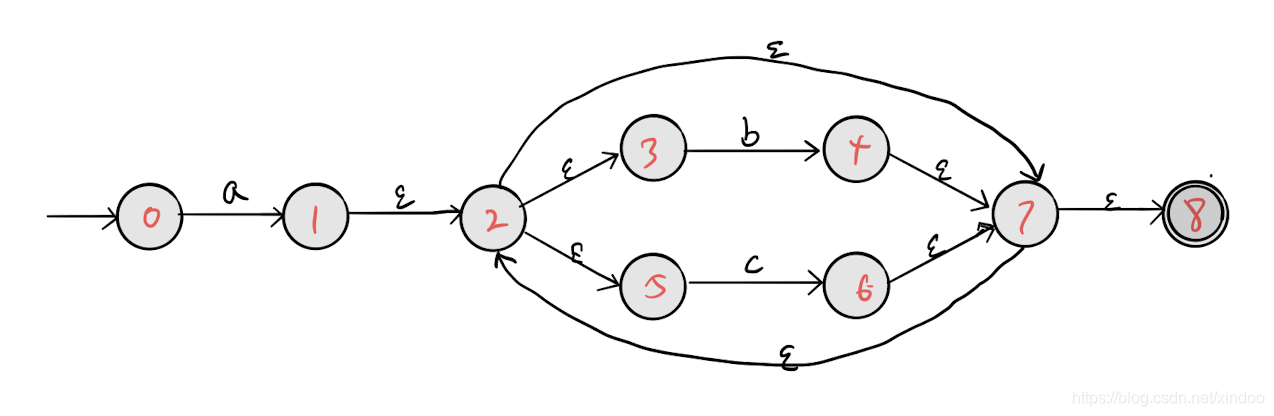
来练习画下 a(c|b)* 的状态图，这里我也给出我画的，你可以参考下。

代码实现

建图

看完上文之后相信你一直知道如果将一个正则表达式转化为状态机的方法了，这里我们要将理论转化为代码。
首先我们要将图转化为代码标识，我用State表示一个节点，其中用了 Map<MatchStrategy, List> next 表示其后继节点，next中有个key-value就是一条边，MatchStrategy用来描述边的信息。

public class State {
    private static int idCnt = 0;
    private int id;
    private int stateType;

    public State() {
        this.id = idCnt++;
    }

    Map<MatchStrategy, List<State>> next = new HashMap<>();

    public void addNext(MatchStrategy path, State state) {
        List<State> list = next.get(path);
        if (list == null) {
            list = new ArrayList<>();
            next.put(path, list);
        }
        list.add(state);
    }
    protected void setStateType() {
        stateType = 1;
    }
    protected boolean isEndState() {
        return stateType == 1;
    }
}

NFAGraph表示一个完整的图，其中封装了对图的操作，比如其中就实现了上文中图串并联和重复的操作（注意我没有实现 {} ）。

public class NFAGraph {
    public State start;
    public State end;
    public NFAGraph(State start, State end) {
        this.start = start;
        this.end = end;
    }

    // |
    public void addParallelGraph(NFAGraph NFAGraph) {
        State newStart = new State();
        State newEnd = new State();
        MatchStrategy path = new EpsilonMatchStrategy();
        newStart.addNext(path, this.start);
        newStart.addNext(path, NFAGraph.start);
        this.end.addNext(path, newEnd);
        NFAGraph.end.addNext(path, newEnd);
        this.start = newStart;
        this.end = newEnd;
    }

    // ϵ
    public void addSeriesGraph(NFAGraph NFAGraph) {
        MatchStrategy path = new EpsilonMatchStrategy();
        this.end.addNext(path, NFAGraph.start);
        this.end = NFAGraph.end;
    }

    // * 重复0-n次
    public void repeatStar() {
        repeatPlus();
        addSToE(); // 重复0
    }

    // ? 重复0次哦
    public void addSToE() {
        MatchStrategy path = new EpsilonMatchStrategy();
        start.addNext(path, end);
    }

    // + 重复1-n次
    public void repeatPlus() {
        State newStart = new State();
        State newEnd = new State();
        MatchStrategy path = new EpsilonMatchStrategy();
        newStart.addNext(path, this.start);
        end.addNext(path, newEnd);
        end.addNext(path, start);
        this.start = newStart;
        this.end = newEnd;
    }

整个建图的过程就是依照输入的字符建立边和节点之间的关系，并完成图的拼接。

private static NFAGraph regex2nfa(String regex) {
    Reader reader = new Reader(regex);
    NFAGraph nfaGraph = null;
    while (reader.hasNext()) {
        char ch = reader.next();
        String edge = null;
        switch (ch) {
            // 子表达式特殊处理
            case '(' : {
                String subRegex = reader.getSubRegex(reader);
                NFAGraph newNFAGraph = regex2nfa(subRegex);
                checkRepeat(reader, newNFAGraph);
                if (nfaGraph == null) {
                    nfaGraph = newNFAGraph;
                } else {
                    nfaGraph.addSeriesGraph(newNFAGraph);
                }
                break;
            }
            // 或表达式特殊处理
            case '|' : {
                String remainRegex = reader.getRemainRegex(reader);
                NFAGraph newNFAGraph = regex2nfa(remainRegex);
                if (nfaGraph == null) {
                    nfaGraph = newNFAGraph;
                } else {
                    nfaGraph.addParallelGraph(newNFAGraph);
                }
                break;
            }
            case '[' : {
                edge = getCharSetMatch(reader);
                break;
            }
            case '^' : {
                break;
            }
            case '$' : {
                break;
            }
            case '.' : {
                edge = ".";
                break;
            }
            // 处理特殊占位符
            case '\\' : {
                char nextCh = reader.next();
                switch (nextCh) {
                    case 'd': {
                        edge = "\\d";
                        break;
                    }
                    case 'D': {
                        edge = "\\D";
                        break;
                    }
                    case 'w': {
                        edge = "\\w";
                        break;
                    }
                    case 'W': {
                        edge = "\\W";
                        break;
                    }
                    case 's': {
                        edge = "\\s";
                        break;
                    }
                    case 'S': {
                        edge = "\\S";
                        break;
                    }
                    // 转义后的字符匹配
                    default:{
                        edge = String.valueOf(nextCh);
                        break;
                    }
                }
                break;
            }
            default : {  // 处理普通字符
                edge = String.valueOf(ch);
                break;
            }
        }
        if (edge != null) {
            NFAState start = new NFAState();
            NFAState end = new NFAState();
            start.addNext(edge, end);
            NFAGraph newNFAGraph = new NFAGraph(start, end);
            checkRepeat(reader, newNFAGraph);
            if (nfaGraph == null) {
                nfaGraph = newNFAGraph;
            } else {
                nfaGraph.addSeriesGraph(newNFAGraph);
            }
        }
    }
    return nfaGraph;
}

这里我用了设计模式中的策略模式将不同的匹配规则封装到不同的MatchStrategy类里，目前我实现了 . \d \D \s \S \w \w，具体细节请参考代码。
这么设计的好处就是简化了匹配策略的添加，比如如果我想加一个 \x 只匹配16进制字符，我只需要加个策略类就好了，不必改很多代码。

匹配

其实匹配的过程就出从起始态开始，用输入作为边，一直往后走，如果能走到终止态就说明可以匹配，代码主要依赖于递归和回溯，代码如下。

public boolean isMatch(String text) {
    return isMatch(text, 0, nfaGraph.start);
}

private boolean isMatch(String text, int pos, State curState) {
    if (pos == text.length()) {
        if (curState.isEndState()) {
            return true;
        }
        return false;
    }
    for (Map.Entry<MatchStrategy, List<State>> entry : curState.next.entrySet()) {
        MatchStrategy matchStrategy = entry.getKey();
        if (matchStrategy instanceof EpsilonMatchStrategy) {
            for (State nextState : entry.getValue()) {
                if (isMatch(text, pos, nextState)) {
                    return true;
                }
            }
        } else {
            if (!matchStrategy.isMatch(text.charAt(pos))) {
                continue;
            }
            // 遍历匹配策略
            for (State nextState : entry.getValue()) {
                if (isMatch(text, pos + 1, nextState)) {
                    return true;
                }
            }
        }
    }
    return false;
}

DFA引擎

上文只是实现了NFA引擎，NFA的引擎建图时间复杂度是O(n)，但匹配一个长度为m的字符串时因为涉及到大量的递归和回溯，最坏时间复杂度是O(mn)。
与之对比DFA引擎的建图时间复杂度O(n^2)，但匹配时没有回溯，所以匹配复杂度只有O(m)，性能差距还是挺大的。
DFA引擎实现的大体流程是先构造NFA(本文内容)，然后用子集构造法将NFA转化为DFA，预计未来我会出一篇博客讲解细节和具体实现。

正则引擎优化

首先DFA引擎是可以继续优化的，使用Hopcroft算法可以进一步将DFA图压缩，更少的状态节点更少的转移边可以实现更好的性能。
其次，目前生产级的正则引擎很多都不是单纯用NFA或者DFA实现的，而是二者的结合，不同正则表达式下用不同的引擎可以达到更好的综合性能，简单说NFA图小但要回溯，DFA不需要回溯但有些情况图会特别大。

DFA和NFA

我们已经多次提到了NFA和DFA，它俩究竟是啥？有啥区别？
首先，NFA和DFA都是有限状态机，都是有向图，用来描述状态和状态之间的关系。
其中NFA全称是非确定性有限状态自动机(Nondeterministic finite automaton)，DFA全称是确定性有限状态自动机(Deterministic finite automaton)。

确定性

二者的差异主要在于确定性和非确定性，何为确定性？
确定性是指面对同一输入，不会出现有多条可行的路径执行下一个节点。有点绕，看完图你就理解了。

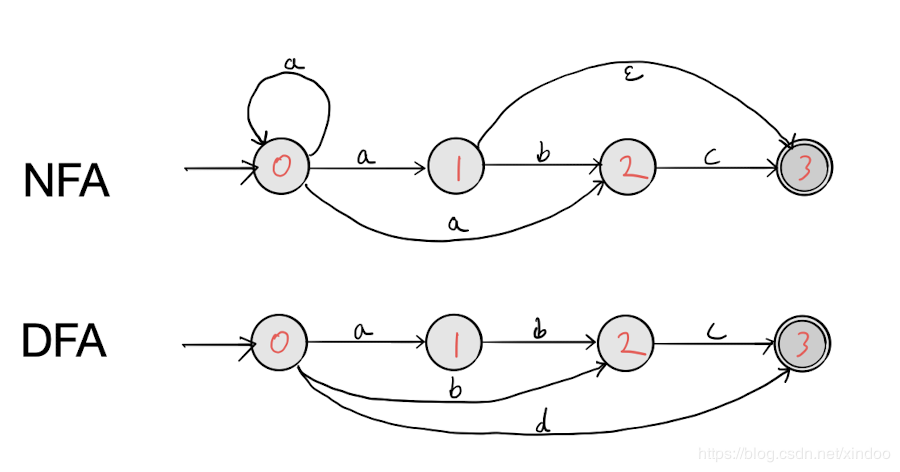
图示分别是一个NFA和DFA，上图之所以是NFA是因为它有节点具备不确定性，比如0节点，在输入”a”之后它分别可以到0 1 2 节点。
还有，上图有 epsilon 边，它可以在没有输入的情况下跳到下一个节点，这也带来了不确定性。相反，下图DFA中，每个节点对某一特定的输入都只有最多一条边。
总结下NFA和DFA的区别就是，有ε边或者某个节点对同一输入对应多个状态的一定是NFA。

等价性

DFA和NFA存在等价性，也就是说任何NFA都可以转化为等价的DFA。
由于NFA的非确定性，在面对一个输入的时候可能有多条可选的路径，所以在一条路径走不通的情况下，需要回溯到选择点去走另外一条路径。
但DFA不同，在每个状态下，对每个输入不会存在多条路径，就不需要递归和回溯了，可以一条路走到黑。
DFA的匹复杂度只有O(n)，但因为要递归和回溯NFA的匹配复杂度达到了O(n^2)。
这也是为什么我们要将引擎中的NFA转化为DFA的主要原因。

NFA转DFA算法

NFA转DFA的算法叫做子集构造法，其具体流程如下。

步骤1: NFA的初始节点和初始节点所有ε可达的节点共同构成DFA的初始节点，然后对初始DFA节点执行步骤2。
步骤2: 对当前DFA节点，找到其中所有NFA节点对输入符号X所有可达的NFA节点，这些节点沟通构成的DFA节点作为当前DFA节点对输入X可达的DFA节点。
步骤3: 如果步骤2中找到了新节点，就对新节点重复执行步骤2。
步骤4: 重复步骤2和步骤3直到找不DFA新节点为止。
步骤5: 把所有包含NFA终止节点的DFA节点标记为DFA的终止节点。

例子

语言描述比较难理解，我们直接上例子。
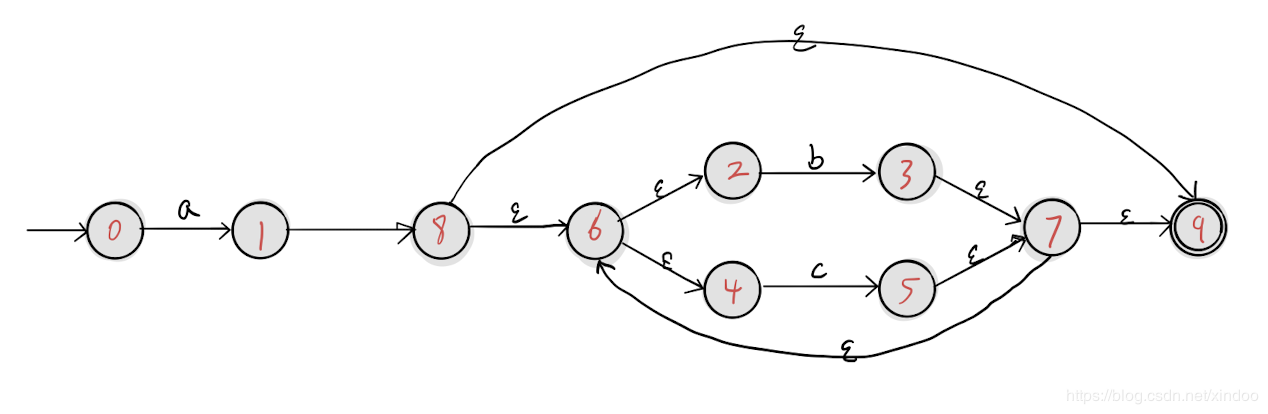
我们已经拿上一篇网站中的正则表达式 a(b|c)* 为例，NFA输出如下。

from	to	input
0->	1	a
1->	8	Epsilon
8->	9	Epsilon
8->	6	Epsilon
6->	2	Epsilon
6->	4	Epsilon
2->	3	b
4->	5	c
3->	7	Epsilon
5->	7	Epsilon
7->	9	Epsilon
7->	6	Epsilon

绘图如下：

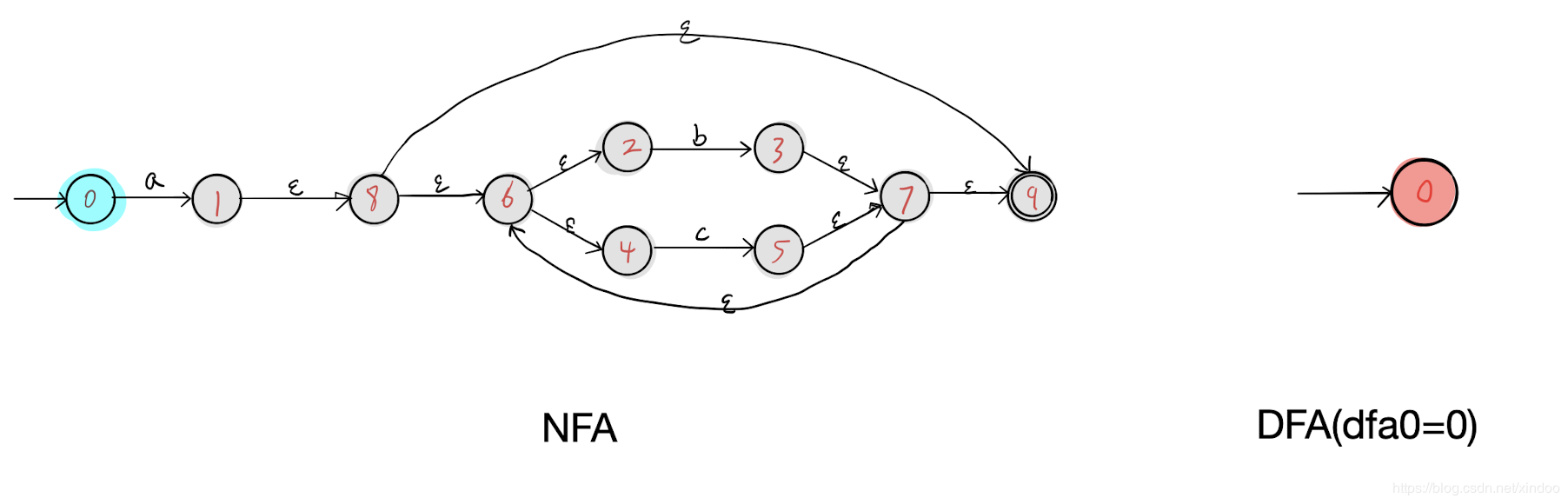
我们在上图的基础上执行步骤1 得到了节点0作为DFA的开始节点。

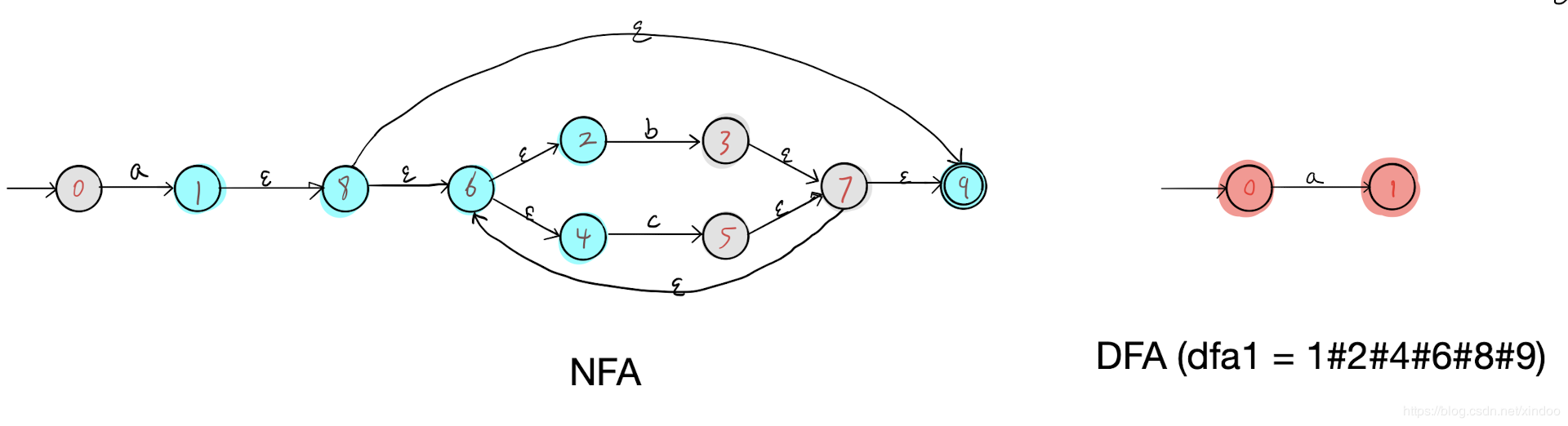
然后对DFA的节点0执行步骤1，找到NFA中所有a可达的NFA节点(1#2#4#6#8#9)构成DFA中的节点1，如下图。

我以dfa1为出发点，发现了b可达的所有NFA节点(2#3#4#6#7#9)和c可达的所有节点(2#4#5#6#7#9)，分别构成了DFA中的dfa2和dfa3，如下图。

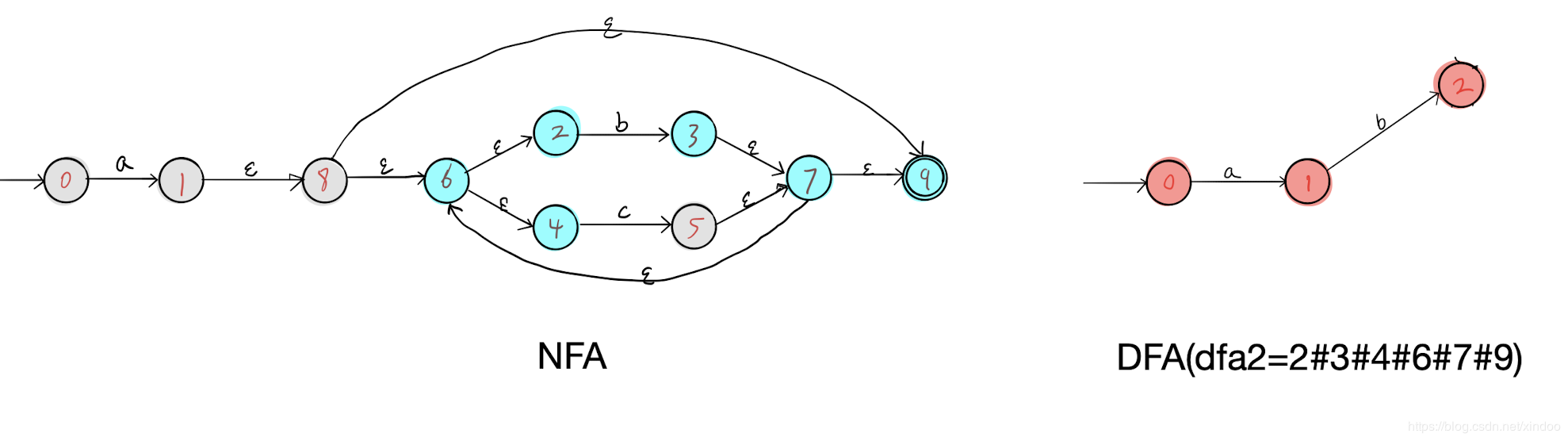
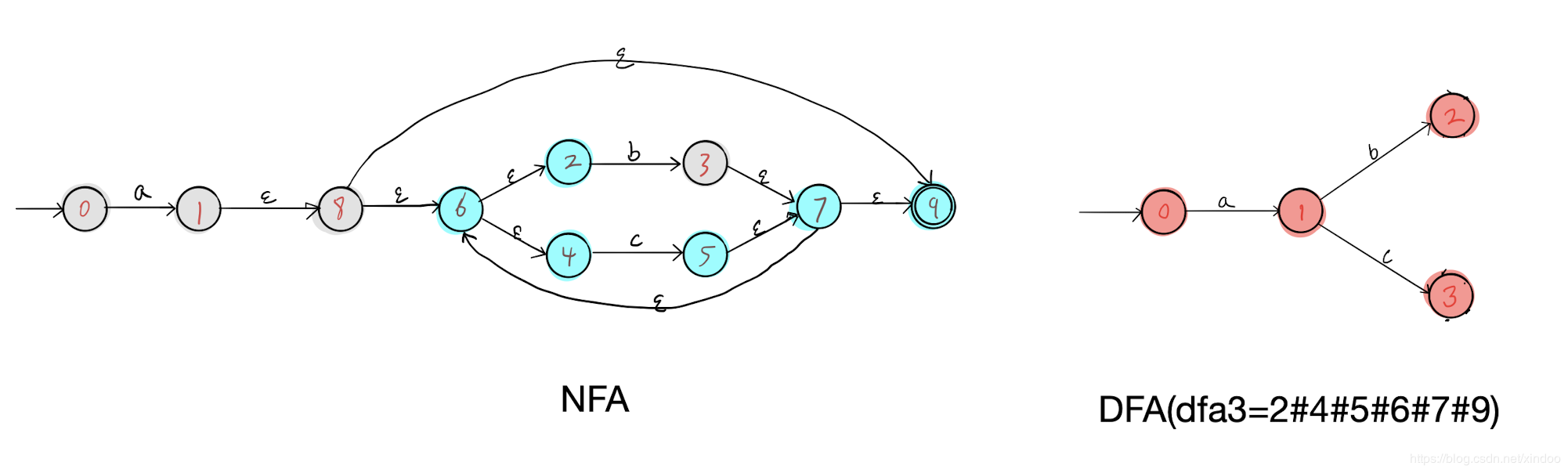
然后我们分别在dfa2 dfa3上执行步骤三，找不到新节点，但会找到几条新的边，补充如下，至此我们就完成了对 a(b|c)* 对应NFA到DFA的转化。

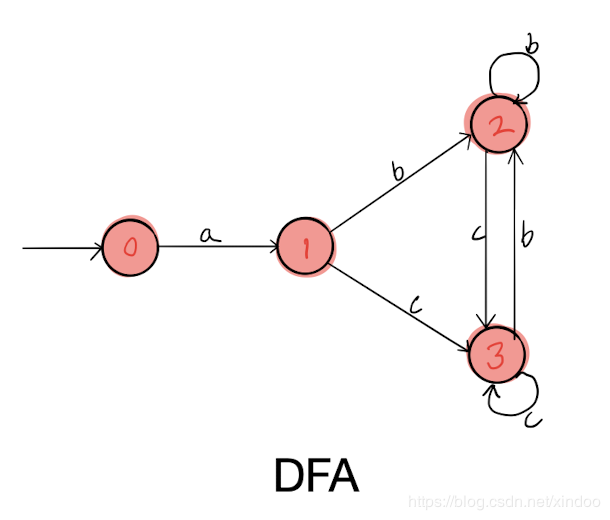
可以看出DFA图节点明显少于NFA，但NFA更容易看出其对应的正则表达式。

代码实现

代码其实就是对上文流程的表述

private static DFAGraph convertNfa2Dfa(NFAGraph nfaGraph) {
       DFAGraph dfaGraph = new DFAGraph();
       Set<State> startStates = new HashSet<>();
       // 用NFA图的起始节点构造DFA的起始节点 步骤1 
       startStates.addAll(getNextEStates(nfaGraph.start, new HashSet<>()));
       if (startStates.size() == 0) {
           startStates.add(nfaGraph.start);
       }
       dfaGraph.start = dfaGraph.getOrBuild(startStates);
       Queue<DFAState> queue = new LinkedList<>();
       Set<State> finishedStates = new HashSet<>();
       // 如果BFS的方式从已找到的起始节点遍历并构建DFA
       queue.add(dfaGraph.start);
       while (!queue.isEmpty()) {  // 步骤2 
           DFAState curState = queue.poll();
           for (State nfaState : curState.nfaStates) {
               Set<State> nextStates = new HashSet<>();
               Set<String> finishedEdges = new HashSet<>();
               finishedEdges.add(Constant.EPSILON);
               for (String edge : nfaState.next.keySet()) {
                   if (finishedEdges.contains(edge)) {
                       continue;
                   }
                   finishedEdges.add(edge);
                   Set<State> efinishedState = new HashSet<>();
                   for (State state : curState.nfaStates) {
                       Set<State> edgeStates = state.next.getOrDefault(edge, Collections.emptySet());
                       nextStates.addAll(edgeStates);
                       for (State eState : edgeStates) {
                           // 添加E可达节点
                           if (efinishedState.contains(eState)) {
                               continue;
                           }
                           nextStates.addAll(getNextEStates(eState, efinishedState));
                           efinishedState.add(eState);
                       }
                   }
                   // 将NFA节点列表转化为DFA节点，如果已经有对应的DFA节点就返回，否则创建一个新的DFA节点
                   DFAState nextDFAstate = dfaGraph.getOrBuild(nextStates);
                   if (!finishedStates.contains(nextDFAstate)) {
                       queue.add(nextDFAstate);
                   }
                   curState.addNext(edge, nextDFAstate);
               }
           }
           finishedStates.add(curState);
       }
       return dfaGraph;
   }

DFAState

public class DFAState extends State {
    public Set<State> nfaStates = new HashSet<>();
    // 保存对应NFAState的id,一个DFAState可能是多个NFAState的集合,所以拼接成String
    private String allStateIds;
    public DFAState() {
        this.stateType = 2;
    }

    public DFAState(String allStateIds, Set<State> states) {
        this.allStateIds = allStateIds;
        this.nfaStates.addAll(states);
         //这里我将步骤五直接集成在创建DFA节点的过程中了
        for (State state : states) {
            if (state.isEndState()) {
                this.stateType = 1;
            }
        }
    }

    public String getAllStateIds() {
        return allStateIds;
    }
}

另外我在DFAGraph中封装了有些NFA节点列表到DFA节点的转化和查找，具体如下。

public class DFAGraph {

    private Map<String, DFAState> nfaStates2dfaState = new HashMap<>();
    public DFAState start = new DFAState();

    // 这里用map保存NFAState结合是已有对应的DFAState, 有就直接拿出来用
    public DFAState getOrBuild(Set<State> states) {
        String allStateIds = "";
        int[] ids = states.stream()
                          .mapToInt(state -> state.getId())
                          .sorted()
                          .toArray();
        for (int id : ids) {
            allStateIds += "#";
            allStateIds += id;
        }
        if (!nfaStates2dfaState.containsKey(allStateIds)) {
            DFAState dfaState = new DFAState(allStateIds, states);
            nfaStates2dfaState.put(allStateIds, dfaState);
        }
        return nfaStates2dfaState.get(allStateIds);
    }
}

DFA引擎匹配过程

dfa引擎的匹配也可以完全复用NFA的匹配过程，所以对之前NFA的匹配代码，可以针对DFA模式取消回溯即可(不取消也没问题，但会有性能影响)。

private boolean isMatch(String text, int pos, State curState) {
    if (pos == text.length()) {
        if (curState.isEndState()) {
            return true;
        }
        for (State nextState : curState.next.getOrDefault(Constant.EPSILON, Collections.emptySet())) {
            if (isMatch(text, pos, nextState)) {
                return true;
            }
        }
        return false;
    }
    for (Map.Entry<String, Set<State>> entry : curState.next.entrySet()) {
        String edge = entry.getKey();
        // 如果是DFA模式,不会有EPSILON边
        if (Constant.EPSILON.equals(edge)) {
            for (State nextState : entry.getValue()) {
                if (isMatch(text, pos, nextState)) {
                    return true;
                }
            }
        } else {
            MatchStrategy matchStrategy = MatchStrategyManager.getStrategy(edge);
            if (!matchStrategy.isMatch(text.charAt(pos), edge)) {
                continue;
            }
            // 遍历匹配策略
            for (State nextState : entry.getValue()) {
                // 如果是DFA匹配模式,entry.getValue()虽然是set,但里面只会有一个元素,所以不需要回溯
                if (nextState instanceof DFAState) {
                    return isMatch(text, pos + 1, nextState);
                }
                if (isMatch(text, pos + 1, nextState)) {
                    return true;
                }
            }
        }
    }
    return false;
}

因为DFA的匹配不需要回溯，所以可以完全改成非递归代码。

private boolean isDfaMatch(String text, int pos, State startState) {
    State curState = startState;
    while (pos < text.length()) {
        boolean canContinue = false;
        for (Map.Entry<String, Set<State>> entry : curState.next.entrySet()) {
            String edge = entry.getKey();
            MatchStrategy matchStrategy = MatchStrategyManager.getStrategy(edge);
            if (matchStrategy.isMatch(text.charAt(pos), edge)) {
                curState = entry.getValue().stream().findFirst().orElse(null);
                pos++;
                canContinue = true;
                break;
            }
        }
        if (!canContinue) {
            return false;
        }
    }
    return curState.isEndState();
}

已所欲，己所从

正则表达式原理及简单实现

有限状态机

状态

字符串匹配

状态机下的正则表达式

串联匹配

并联匹配

重复匹配(正则表达式中的 ? + *)

特殊符号(正则表达式中的 . \d \s……)

子表达式(正则表达式 () )

练习题

代码实现

建图

匹配

DFA引擎

正则引擎优化

DFA和NFA

确定性

等价性

NFA转DFA算法

例子

代码实现

DFA引擎匹配过程